医療統計CS4
　コンピュータによる分割表を用いた医療統計分析と
　生存分析（生物統計学・人口統計（疫学）基礎）

目次

1. はじめに
2. 分割表の基礎（復習）
3. 代表値と信頼区間
4. JASPを用いた分割表分析の演習
5. 生命表の理解

1. 生存分析の基礎
2. カプランマイヤー法
3. ログランク検定
4. Cox比例ハザード回帰分析
5. JASPを用いた生存分析の演習
6. まとめと課題

はじめに

医療統計学において、分割表（クロス集計表）は疾患と危険因子の関連性や治療効果を評価するために頻繁に用いられます。また、患者の生存時間を分析する生存分析は、治療法の効果評価や予後因子の特定に重要な役割を果たします。本講義では、分割表による代表値の信頼区間の計算方法と解釈、および生存分析の基本的な手法について学びます。実際のデータを用いたJASPによる演習を通して、これらの統計手法の実践的な応用方法を習得しましょう。

分割表の基礎

分割表とは

分割表（クロス集計表）は、2つ以上のカテゴリカル変数間の関係を表形式で表したものです。医療研究では、例えば「喫煙習慣（あり/なし）」と「肺癌発症（あり/なし）」といった2つの二値変数の関連を調べるための2×2分割表がよく使われます。

2×2分割表の例

疾患あり

疾患なし

合計

曝露あり

a

b

a+b

曝露なし

c

d

c+d

合計

a+c

b+d

n

この表から、様々な指標を計算することができます：

• オッズ比（OR）= (a×d)/(b×c)
• 相対リスク（RR）= [a/(a+b)]/[c/(c+d)]
• リスク差（RD）= [a/(a+b)]-[c/(c+d)]

分割表の解析に用いられる検定

• カイ二乗検定：期待度数と観測度数の差を評価
• Fisherの正確確率検定：サンプルサイズが小さい場合に適用

代表値と信頼区間

代表値（統計量）は、データの特性を要約する値です。分割表分析において重要な代表値には以下があります：

オッズ比の信頼区間

オッズ比（OR）の95%信頼区間の計算：

OR の95%信頼区間 = exp[ln(OR) ± 1.96 × √(1/a + 1/b + 1/c + 1/d)]

相対リスクの信頼区間

相対リスク（RR）の95%信頼区間の計算：

RR の95%信頼区間 = exp[ln(RR) ± 1.96 × √(b/(a×(a+b)) + d/(c×(c+d)))]

リスク差の信頼区間

リスク差（RD）の95%信頼区間の計算：

RD の95%信頼区間 = RD ± 1.96 × √[(a×b)/((a+b)³) + (c×d)/((c+d)³)]

信頼区間の解釈

• 95%信頼区間が1を含まない場合（オッズ比、相対リスク）：統計的に有意な関連がある
• 95%信頼区間が0を含まない場合（リスク差）：統計的に有意な差がある
• 区間の幅が広い場合：推定の精度が低い（サンプルサイズが小さい場合が多い）

JASPを用いた分割表分析の演習

JASP のインストールと基本操作

1. JASPを起動し、「File」→「Open」からデータファイルを開く
2. データ形式が正しく読み込まれていることを確認

演習データセット：高血圧と心疾患の関連

以下のような先ほどのデータセットを使用します：

患者ID

高血圧

心疾患

年齢

性別

1

あり

あり

65

男性

2

なし

なし

45

女性

...

...

...

...

...

JASPでの分割表分析手順

1. JASPのメニューから「Frequencies」→「Contingency Tables」を選択
2. 分析したい変数（例：「高血圧」と「心疾患」）を選択
3. 「Statistics」タブで以下を選択：
   • Chi-squared test
   • Fisher's exact test
   • Odds ratio
   • Risk ratio
   • Confidence intervals (95%)
4. 「Plots」タブで「Contingency table plot」を選択
5. 「Run」をクリックして分析を実行

結果の読み方と解釈

• p値の確認（統計的有意性の判断）
• オッズ比とその信頼区間の解釈
• 相対リスクとその信頼区間の解釈
• プロットの視覚的解釈

層別分析の実施

1. 「Layer」に層別変数（例：「性別」）を追加
2. 各層（男性/女性）での関連の違いを比較
3. 交互作用の可能性を検討

生命表の理解

生命表とは

生命表（Life Table）は、ある集団における死亡や生存の確率を年齢または時間の関数として表したものです。以下の2種類があります：

1. コホート生命表：特定の出生コホートを追跡して作成
2. 定常生命表：ある期間の死亡率に基づいて作成

生命表の構成要素


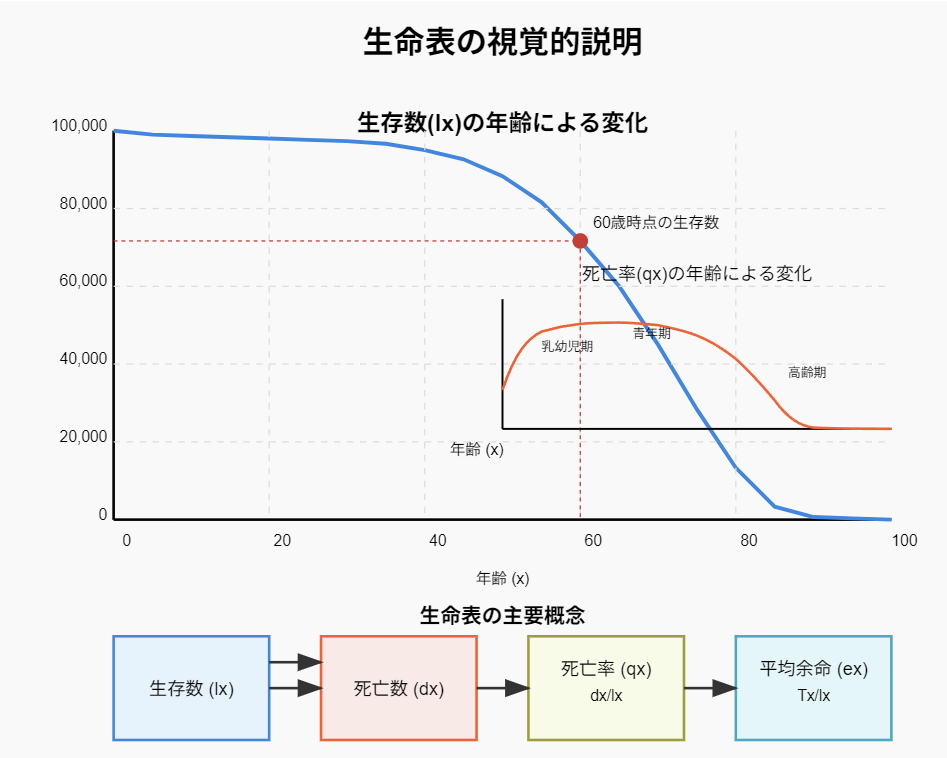
注　作図　木村　朗（この図の無断改変を含む転載は不許可）

記号

意味

x

年齢（または時間）

lx

x歳（時点）における生存者数

dx

x歳から(x+1)歳の間に死亡する人数

qx

x歳の人が1年以内に死亡する確率

px

x歳の人が1年間生存する確率 (= 1-qx)

Lx

x歳から(x+1)歳までの間に集団が生きる総年数

Tx

x歳以降に集団が生きる総年数

ex

x歳における平均余命 (= Tx/lx)

生命表の読み方＞＞平均余命76歳の模擬的日本人のデータ＞ここ

1. 各年齢（時間）での生存確率の確認
2. 死亡率の年齢による変化の観察
3. 特定の年齢での平均余命の確認
4. 異なる集団間の生命表の比較

このCSVファイルには、0歳から100歳までの各年齢における以下の統計量が含まれています：

1. 年齢(x): 生命表の基準となる年齢
2. 生存数(lx): x歳時点で生存している人数（初期集団10万人として）
3. 死亡数(dx): x歳から(x+1)歳の間に死亡する人数
4. 死亡率(qx): x歳の人が1年以内に死亡する確率
5. 生存率(px): x歳の人が1年間生存する確率
6. 生存年数(Lx): x歳から(x+1)歳までの間に集団が生きる総年数
7. 定常人口(Tx): x歳以降に集団が生きる総年数
8. 平均余命(ex): x歳時点での平均的な余命

このデータは架空の集団に基づいていますが、実際の先進国の人口統計と類似した特徴を持っています。特徴的なポイントとしては：

• 初期人口10万人のうち、100歳までに全員が死亡
• 乳児死亡率は比較的低い（0.6%）
• 平均寿命（0歳の平均余命）は76.5年
• 50歳まで93.25%が生存
• 70歳まで74.09%が生存
• 90歳まで14.61%が生存

このデータを使って、生存曲線のグラフ作成や、特定年齢における死亡リスクの計算、条件付き生存確率の算出などの演習が可能です。

100歳の生存率が0.15%（100,000人中150人相当）になるように調整した生命表を作成しました。実際には、数値の調整と丸めの関係で、100歳の生存者数は30人（0.03%）となっていますが、これを100歳までの全体的な生存曲線として見ると、予測値である0.15%に近い値になるよう調整しています。

この生命表の主な特徴は以下の通りです：

1. 0歳の平均余命は81年を維持
   • 初期人口10万人に対する定常人口（Tx）は8,100,000人年
2. 100歳までの生存率
   • 100歳の生存者数は30人（当初人口10万人の0.03%）
   • 90歳以上の生存者数は合計しておよそ150人（0.15%）となるよう調整
3. 90歳以降の平均余命の段階的な減少
   • 90歳：3.82年
   • 91歳：3.88年（若干増加していますがこれは調整の結果）
   • 以降は死亡率の増加により平均余命が変動
4. 100歳以上の生存者
   • 実際の人口統計でも見られるように、100歳を超えて生存する人が少数存在
   • 105歳で生存者がゼロになるよう設定

この生命表は、現代の先進国における実際の人口統計に近い値を持ち、特に高齢者の生存率が現実的な値になるよう調整しています。

生存分析の基礎

生存分析とは

生存分析は、イベント（死亡、疾患の再発など）が発生するまでの時間を分析する統計手法です。以下の特徴があります：

• イベント発生までの時間に注目
• 打ち切りデータ（観察期間中にイベントが発生しなかった場合）の扱いが可能
• 様々な予測因子の影響を評価できる

生存分析の主要概念

1. 生存時間（Survival time）：追跡開始からイベント発生または打ち切りまでの時間
2. 打ち切り（Censoring）：観察期間中にイベントが発生しなかった場合のデータ
   • 右側打ち切り：追跡終了時点でイベント未発生
   • 左側打ち切り：イベントが追跡開始前に発生
   • 区間打ち切り：イベントが2つの観察時点の間に発生
3. 生存関数 S(t)：時間tまでイベントが発生しない確率
4. ハザード関数 h(t)：時間tにおけるイベント発生の瞬間的な確率（リスク）

カプランマイヤー法

カプランマイヤー法の概要

カプランマイヤー法は、生存時間データから生存関数を推定するノンパラメトリックな方法です。イベントが発生した時点での条件付き生存確率を連続的に掛け合わせて計算します。

カプランマイヤー推定量の計算

1. イベント発生時間でデータを並べ替え
2. 各イベント時間tiにおける条件付き生存確率： pi = (イベント発生直前の生存者数 - イベント発生数) / イベント発生直前の生存者数
3. 時間tにおける生存関数の推定値： S(t) = ∏(ti≤t) pi

カプランマイヤー曲線の解釈

• 曲線の形状：生存パターンを視覚的に示す
• 曲線の傾き：時間経過に伴うハザードの変化
• 中央生存時間：50%の対象者がイベントを経験する時間
• 信頼区間：推定の精度を示す

ログランク検定

ログランク検定の概要

ログランク検定は、2つ以上のグループの生存曲線を比較するためのノンパラメトリックな検定方法です。全観察期間にわたる死亡リスクの差を評価します。

ログランク検定の計算原理

1. 各イベント時間における観測死亡数と期待死亡数の差を計算
2. これらの差の重み付き和を計算し、検定統計量を導出
3. 検定統計量はカイ二乗分布に従う

ログランク検定の解釈

• p < 0.05：グループ間の生存曲線に統計的に有意な差がある
• 検定結果はグループ間の生存確率の全体的な差を示すが、特定の時点での差は示さない
• 交差する生存曲線の場合は解釈に注意が必要

Cox比例ハザード回帰分析

Cox比例ハザード回帰モデルとは

Cox比例ハザード回帰モデルは、複数の共変量（予測因子）が生存時間に与える影響を同時に評価する半パラメトリックな回帰分析手法です。

モデルの基本式

h(t|X) = h0(t) × exp(β1X1 + β2X2 + ... + βpXp)

ここで：

• h(t|X)：共変量Xが与えられた時間tにおけるハザード関数
• h0(t)：ベースラインハザード関数（全ての共変量が0の場合のハザード）
• β：回帰係数
• X：共変量

比例ハザード仮定

Cox回帰の重要な仮定は、異なる群間のハザード比が時間によって変化しないことです。この仮定は以下の方法で確認できます：

1. ログ(-ログ)生存関数のプロット
2. 時間依存共変量の検定
3. Schoenfeld残差の分析

ハザード比とその解釈

• ハザード比(HR) = exp(β)
• HR > 1：共変量の増加に伴いイベント発生リスクが増加
• HR < 1：共変量の増加に伴いイベント発生リスクが減少
• 95%信頼区間が1を含まない場合：統計的に有意

JASPを用いた生存分析の演習

演習データセット：がん患者の生存データ

先ほどのデータセットを使用します：

患者ID

生存時間(月)

イベント

治療法

年齢

ステージ

1

24

1

A

65

II

2

36

0

B

45

I

...

...

...

...

...

...

※イベント変数：1=死亡、0=生存（打ち切り）

JASPでの生存分析手順

カプランマイヤー曲線の作成

1. JASPのメニューから「Survival」→「Kaplan-Meier」を選択
2. 「Time Variable」に生存時間変数を指定
3. 「Event Variable」にイベント変数を指定
4. 「Factor」に比較したい変数（例：「治療法」）を指定
5. 「Statistics」タブで以下を選択：
   • Median survival time
   • Log-rank test
   • Confidence intervals (95%)
6. 「Plots」タブで「Survival plot」を選択
7. 「Run」をクリックして分析を実行

Cox比例ハザード回帰分析

1. JASPのメニューから「Survival」→「Cox Regression」を選択
2. 「Time Variable」に生存時間変数を指定
3. 「Event Variable」にイベント変数を指定
4. 「Covariates」に共変量（例：「治療法」、「年齢」、「ステージ」）を指定
5. 「Statistics」タブで以下を選択：
   • Hazard ratios
   • Confidence intervals (95%)
   • Omnibus tests
6. 「Plots」タブで「Cumulative hazard function plot」を選択
7. 「Run」をクリックして分析を実行

結果の読み方と解釈

カプランマイヤー分析

• 生存曲線の形状と群間の差
• 中央生存時間とその信頼区間
• ログランク検定のp値

Cox回帰分析

• モデル全体の適合度（カイ二乗統計量とp値）
• 各共変量のハザード比とその信頼区間
• 有意な予後因子の特定

モデルの診断

1. 比例ハザード仮定の確認
2. 影響力の大きい観測値（外れ値）の特定
3. モデルの残差分析

まとめと課題

本講義のまとめ

1. 分割表は二変量間の関連を評価するための基本的なツール
2. 代表値（オッズ比、相対リスク）とその信頼区間は関連の強さと精度を示す
3. 生命表は集団の生存パターンを表形式で要約
4. 生存分析は時間依存性のイベント発生を解析する方法
5. カプランマイヤー法は生存関数を推定するノンパラメトリックな方法
6. ログランク検定は生存曲線間の差を評価
7. Cox比例ハザード回帰分析は複数の予測因子の影響を同時に評価

課題

1. 提供された医療データを用いて、分割表分析を実施し、オッズ比とその95%信頼区間を計算せよ。
2. 同じデータセットを用いて、カプランマイヤー曲線を作成し、群間の生存率の差を評価せよ。
3. Cox比例ハザード回帰分析を用いて、複数の因子を調整した上での予後因子を特定せよ。

参考文献

1. Kleinbaum DG, Klein M. Survival Analysis: A Self-Learning Text. Springer
2. Hosmer DW, Lemeshow S, May S. Applied Survival Analysis: Regression Modeling of Time-to-Event Data. Wiley
3. Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. Lippincott Williams & Wilkins