🎯 DAG分析の実践ガイド
媒介変数・交絡要因・コライダーの適切な処理法
SPSS・JASP対応の具体的手法とアルゴリズム
📚 三つの重要概念の理解
定義: XがYに与える影響の経路(メカニズム)
処理: 媒介分析で効果を分解
注意: コントロールすると効果が消える
定義: XとYの両方に影響する第三変数
処理: 統計モデルに含めて調整
注意: 無視すると偽の関連
定義: XとYから影響を受ける変数
処理: 統計モデルに含めない
注意: 調整すると偽の関連が生まれる
🔬 処理方法の決定アルゴリズム
📋 DAGベース変数処理アルゴリズム
| 変数タイプ | 識別方法 | 処理方針 | 統計手法 | 解釈上の注意 |
|---|---|---|---|---|
| 媒介変数 | X → M → Y の経路上 | 媒介分析実行 | Bootstrap法、Sobel検定 | 直接効果と間接効果を分離 |
| 交絡要因 | C → X, C → Y | 統計モデルに含めて調整 | 重回帰分析、層別分析 | 調整後の効果を解釈 |
| コライダー | X → L ← Y | 統計モデルに含めない | 単回帰分析(コライダー除外) | 選択バイアスに注意 |
🎯 統計手法の理論的根拠と実践的メカニズム
📈 1. 媒介分析:なぜBootstrap法とSobel検定が有効なのか?
理論的背景: 媒介効果は「間接効果 = a×b」として計算されるが、この積の分布は正規分布に従わない。従来のt検定では正確な信頼区間が得られない。
Bootstrap法のメカニズム:
- リサンプリング:元データから復元抽出で5000回以上のサンプルを作成
- 間接効果の分布推定:各サンプルでa×bを計算し、実際の分布形状を把握
- ノンパラメトリック信頼区間:分布の2.5%と97.5%点から95%CIを算出
- 結果の判定:信頼区間に0が含まれなければ間接効果が有意
Sobel検定との比較: Sobel検定は正規分布を仮定するが、Bootstrap法は分布を仮定しないため、小サンプルや非正規分布でも正確。現在の金標準はBootstrap法。
実践的価値: 直接効果(c')と間接効果(ab)を分離することで、「効果があるか」だけでなく「なぜ効果があるのか」というメカニズムを解明できる。
⚖️ 2. 交絡調整:なぜ重回帰分析で「統計的にコントロール」できるのか?
理論的背景: 交絡要因Cが存在すると、X→Yの関係にC→X、C→Yの影響が混入し、真の因果効果が歪む。統計的調整により、Cの影響を「一定に保った状態」でのX→Y効果を推定する。
重回帰分析のメカニズム:
- 偏回帰係数の意味:Y = β₀ + β₁X + β₂C + ε において、β₁は「Cが同じ値の個体間でのXの効果」
- 残差による調整:CでXとYをそれぞれ回帰し、その残差同士の関係を見ることと等価
- 条件付き独立性:Cを条件として与えると、XとYの間にCを通る経路以外の関連が明確になる
- マッチング効果:統計的には、Cの値が同じ個体同士を比較することに相当
層別分析との関係: 重回帰分析は「連続的な層別分析」。Cを離散カテゴリーに分けて各層内でX→Y効果を見る層別分析の一般化版。
実践的価値: 観察研究において、ランダム化ができない状況で疑似的な「統制群」を作り出し、因果推論を可能にする。ただし、未測定交絡要因は除去できない限界がある。
🚫 3. コライダー除外:なぜ「調整しない」ことが重要なのか?
理論的背景: コライダーL(X→L←Y)を統計モデルに含めると、本来独立だったXとYの間に人工的な関連(collider bias)が生まれる。これは「条件付け効果」として知られる現象。
コライダーバイアスのメカニズム:
- 選択効果:Lの特定の値を持つ個体だけを分析すると、XとYが高い個体とXとYが低い個体が混在
- 逆相関の発生:L=一定の条件下では、Xが高い→Yは相対的に低い、という負の相関が人工的に発生
- 見かけの関連:真の因果関係がなくても、統計的に有意な関連が検出される
- バークソンのパラドックス:病院での研究で「病気AとBに負の相関がある」ように見える現象と同じ
具体例で理解: 「運動能力」と「学力」が「進学校合格」に影響する場合、進学校の生徒だけを分析すると運動能力と学力に負の相関が見える。実際は無関係でも、「どちらかが優秀なら合格」という選択効果によるもの。
対処法: コライダーを統計モデルに含めず、単回帰分析または完全に除外した分析を行う。サンプル選択時にもコライダーによる絞り込みを避ける。
実践的価値: 研究結果の妥当性を保つ。特に観察研究では、既存データベースや特定集団のデータを用いる際に、選択バイアスを防ぐ重要な原則。
🎯 統合的理解:DAGによる因果推論の威力
これら3つの処理法は、すべて「因果関係の方向性」に基づいて決定される。DAGを正しく描くことで、どの変数をどう扱うべきかが論理的に決まり、恣意的な分析を避けることができる。統計は「道具」であり、DAGは「設計図」。正しい設計図なしに適切な道具は選べない。
💻 ソフトウェア別実装方法
🔵 SPSS での実装
1. 媒介分析(PROCESS Macro使用)
2. 交絡要因の調整(重回帰分析)
3. コライダーの扱い
- PROCESS Macroは別途インストールが必要(Hayes, 2022)
- 媒介分析では必ずBootstrap法を使用
- 交絡調整では多重共線性をVIFで確認
🟢 JASP での実装
1. 媒介分析
2. 重回帰分析(交絡調整)
- GUIベースで直感的
- ベイズ統計も同時実行可能
- 結果が自動的にAPA形式
🔴 R での実装(参考)
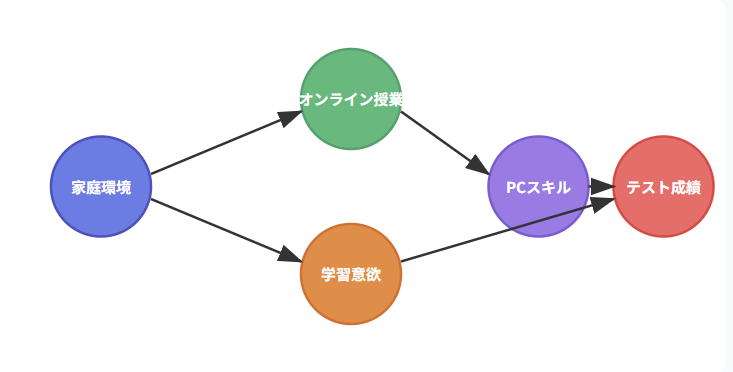
📊 具体例:教育効果研究
⚠️ よくある間違いと対策
🚫 絶対に避けるべき間違い
- 媒介変数をコントロール → 効果の経路を遮断してしまう
- 交絡要因を統計モデルに含めない → 偽の因果関係を結論づける
- コライダーを統計モデルに含める → 存在しない関連を作り出す
- DAGを描かずに分析 → 変数の役割を誤解する
✅ ベストプラクティス
- 事前にDAGを描く - 分析前に変数関係を明確化
- 専門知識を活用 - 統計だけでなく領域知識も重要
- 感度分析を実行 - 異なる仮定での結果を確認
- Bootstrap法を使用 - 媒介分析では特に重要
📈 効果量の解釈ガイド
媒介分析の効果分解
c = c' + ab
| 効果の種類 | 意味 | 解釈の仕方 | 重要度の判断 |
|---|---|---|---|
| 直接効果 (c') | 媒介変数を通さない直接的影響 | 他の要因を除いた純粋な効果 | 統計的有意性とCIで判断 |
| 間接効果 (ab) | 媒介変数を通じた間接的影響 | メカニズムを示す重要な指標 | Bootstrap CIが0を含まない |
| 総効果 (c) | 全体的な影響の大きさ | 実践的意義を判断する基準 | 効果量の大きさで判断 |
🎓 実践チェックリスト
📋 分析実行前チェックリスト
🔍 分析設計段階
- ☐ 理論的背景に基づくDAG作成
- ☐ 各変数の役割を明確化
- ☐ サンプルサイズの妥当性確認
- ☐ 測定尺度の適切性確認
📊 分析実行段階
- ☐ 前提条件の確認(正規性等)
- ☐ 多重共線性の診断
- ☐ 外れ値の検出と処理
- ☐ 適切な統計手法の選択
📝 結果解釈段階
- ☐ 効果量の実践的意義
- ☐ 信頼区間の幅と意味
- ☐ 感度分析の実施
- ☐ 限界と今後の課題