信頼区間の基本
はじめに:信頼区間って何?
「平均身長は170cm」と言われたら、それだけで十分な情報でしょうか?実は、そのデータがどれだけ信頼できるかを知ることも大切です。ここで登場するのが信頼区間です。
信頼区間とは、「真の値がこの範囲内にある確率が高い」と言える範囲のことです。例えば「平均身長は170±2cm(95%信頼区間)」と言われれば、「真の平均身長が168〜172cmの範囲内にある確率が95%である」という意味になります。

信頼区間の基本的な考え方
なぜ必要なの?
私たちが調べられるのは、いつも標本(サンプル)の一部だけです。例えば:
日本人全員(約1億2千万人)の血圧を測ることは不可能ですよね。そのため、1000人だけ測って、その平均値から「日本人の平均血圧はおよそ120mmHg」と推測します。
でも、別の1000人を選んだら、平均値は少し違うかもしれません。そこで信頼区間を使うと、「真の平均値はこのくらいの範囲内にあるはず」と推測できるのです。
確率との関係
信頼区間は確率の考え方を使っています。95%信頼区間とは、「同じ方法で100回調査したら、95回はこの区間内に真の値が含まれる」という意味です。
ポイント:信頼区間は「真の値が固定されていて、区間が変動する」と考えます。これは、私たちが標本を変えるたびに、計算される区間も変わるからです。
信頼区間の計算方法:ステップバイステップ
平均値を計算する
まず、あなたの標本(データ)の平均値を計算します。
標準偏差を計算する
標準偏差は、データのばらつき具合を示す数値です。
計算が難しいときは、電卓やエクセルなどのツールを使っても大丈夫です!
標準誤差を計算する
標準誤差は、平均値の精度を示す指標です。
信頼区間を計算する
95%信頼区間を求めるには、標準誤差に「1.96」をかけます。
「1.96」という数字は、正規分布から来ています。他の信頼水準なら別の数字を使います:
- 90%信頼区間:1.645を使う
- 95%信頼区間:1.96を使う
- 99%信頼区間:2.58を使う
例:血圧測定の例
100人の血圧を測定したところ:
- 平均値:120 mmHg
- 標準偏差:15 mmHg
では、95%信頼区間を求めてみましょう:
- 標準誤差 = 15 ÷ √100 = 15 ÷ 10 = 1.5 mmHg
- 95%信頼区間 = 120 ± (1.96 × 1.5)
- 95%信頼区間 = 120 ± 2.94
- 95%信頼区間 = [117.06, 122.94] mmHg
つまり、「母集団の真の平均血圧は117.06~122.94 mmHgの範囲内にある確率が95%」ということです。
信頼区間を直感的に理解する

信頼区間を広げると信頼度は上がりますが、精度は下がります。逆に狭めると精度は上がりますが、信頼度は下がります。
重要:信頼区間を狭くするには?
- サンプルサイズを大きくする(データをたくさん集める)
- より正確な測定方法を使う(ばらつきを減らす)
サンプルサイズと信頼区間の関係
グラフから分かるように、サンプルサイズ(標本の大きさ)が大きくなるほど信頼区間(縦軸)は狭くなり、より精度の高い推定ができます。
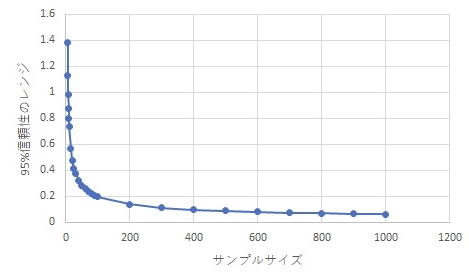
100を超えるとかなり限界に近づく
もっと数式と合わせて知りたい人は こちらをどうぞコピペでドン
https://www.youtube.com/watch?v=wYangfrCQYM
医療分野での信頼区間の応用例
新薬の効果測定
ある新薬の効果を調べるために、100人の患者さんに薬を投与したとします。血圧低下の平均が10 mmHgで、95%信頼区間が[8, 12] mmHgだった場合:
- 「血圧が平均10 mmHg下がった」という結果だけでなく
- 「真の効果は8~12 mmHgの間にある確率が95%」ということも分かります
これにより、医師はより正確に薬の効果を判断できます。
検査値の解釈
血液検査で、あるタンパク質の正常値が「5±1.5(95%信頼区間)」と示されていれば:
- 平均値は5
- 真の平均値は3.5~6.5の範囲内にある確率が95%
つまり、患者さんの値がこの範囲内なら「正常」と判断できます。
| 疾患 | 測定値の平均 | 95%信頼区間 | 解釈 |
|---|---|---|---|
| 高血圧症 | 150 mmHg | [145, 155] | 明らかに高値(正常:140未満) |
| 貧血 | 11.0 g/dL | [10.5, 11.5] | 境界域(正常:12.0以上) |
| 血糖値 | 120 mg/dL | [115, 125] | ほぼ正常範囲(正常:126未満) |
まとめ:信頼区間の大切なポイント
- 単なる点推定ではなく、区間で考える:一点の推定値だけでなく、「この範囲内にある可能性が高い」と考えることが大切です。
- サンプルサイズが重要:データが多いほど、信頼区間は狭くなり、より正確な推定ができます。
- 95%信頼区間が最もよく使われる:医学研究では、95%信頼区間が標準的です。
- 信頼区間はデータの質によって変わる:測定方法が正確でないと、信頼区間は広くなります。
ヒント:信頼区間は「この区間に真の値が入っている」と言っているのではなく、「もし何度も調査を繰り返したら、95%(または選んだ確率)の頻度でこの区間に真の値が含まれる」と言っています。この微妙な違いを理解することが大切です。